Dobrzy menedżerowie muszą nie tylko być w stanie zrozumieć koncepcyjne podstawy zachowań kosztowych, ale muszą także być w stanie zastosować te koncepcje do rzeczywistych danych, które nie zawsze zachowują się w oczekiwany sposób. Na dane o kosztach mają wpływ złożone interakcje. Weźmy na przykład koszty eksploatacji pojazdu. Z koncepcyjnego punktu widzenia zużycie paliwa jest zmiennym kosztem napędzanym przez kilometry. Jednak efektywność zużycia paliwa może się zmieniać w zależności od liczby kilometrów autostrad w porównaniu do mil miejskich. Ponadto opony zużywają się szybciej przy wyższych prędkościach, hamulce bardziej cierpią z powodu jazdy w mieście i tak dalej. Ubezpieczenie pojazdu jest traktowane jako koszt stały; ale porcje są wymagane (ubezpieczenie od odpowiedzialności), a niektóre porcje nie są (ubezpieczenie od kolizji). Ponadto, jeśli masz wrak, dostałeś mandat, koszt ubezpieczenia może wzrosnąć. Chodzi o to, że ocena rzeczywistego charakteru zachowania kosztowego może być bardziej zniechęcająca, niż można się było spodziewać. Niemniej jednak kierownictwo musi zrozumieć zachowanie kosztów, co czasami wymaga nieco pracy księgowej. Zacznijmy od rozważenia przypadku „kosztów mieszanych”.
Koszty mieszane
Wiele kosztów zawiera zarówno zmienne, jak i stałe komponenty. Koszty te nazywane są mieszanymi lub częściowo zmiennymi. Jeśli masz telefon komórkowy, prawdopodobnie wiesz o takich rzeczach więcej niż chcesz. Umowy na telefony komórkowe zwykle przewidują miesięczną opłatę plus opłaty za użytkowanie za nadwyżki minut, wiadomości SMS i tak dalej. Przy koszcie mieszanym istnieje pewna stała kwota plus zmienny składnik związany z działaniem. Koszty mieszane są trudniejsze do oszacowania, ponieważ zmieniają się w odpowiedzi na zmiany wolumenu. Ale element kosztów stałych oznacza, że ogólna zmiana nie jest wprost proporcjonalna do zmiany działalności.
Metoda wysoka-niska
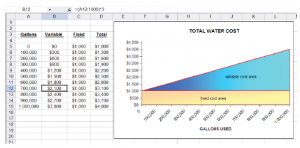
Jednym z podejść do rozdzielania kosztów mieszanych jest metoda wysoka-niska. Jest to być może najprostsza technika dzielenia kosztu mieszanego na części stałe i zmienne. Należy jednak pamiętać, że może zwrócić nieprecyzyjną odpowiedź, jeśli analizowany zestaw danych zawiera wiele fałszywych punktów danych. Ale będzie działał dobrze w innych przypadkach, podobnie jak w przypadku rachunków za wodę w Butler’s Car Wash. Informacje z faktycznych rachunków za wodę w Butler są pokazane w prawym górnym rogu. Butler jest ciekawy, ile wyniesie sierpniowy rachunek za wodę, jeśli zużyje się 650 000 galonów. Załóżmy, że jedyne dostępne dane pochodzą z wyżej wymienionych czterech rachunków za wodę. Dzięki technice wysoka-niska najwyższy i najniższy poziom aktywności są identyfikowane na pewien okres czasu. Najwyższy rachunek za wodę wynosi 3550 USD, a najniższy 2020 USD. Różnica w koszcie między najwyższym i najniższym poziomem aktywności reprezentuje koszt zmienny (3550 USD – 2020 USD = 1530 USD) związany ze zmianą aktywności (850 000 galonów w górnej części i 340 000 galonów w dolnej części daje różnicę 510 000 galonów). Różnica kosztów jest dzielona przez różnicę aktywności w celu ustalenia kosztu zmiennego dla każdej dodatkowej jednostki aktywności (1 530 USD / 510 tysięcy galonów = 3 USD za tysiąc). Koszt stały można obliczyć odejmując koszt zmienny (koszt zmienny na jednostkę pomnożony przez poziom aktywności) od kosztu całkowitego. Tabela powyżej po prawej pokazuje zastosowanie metody high-low. Elektroniczny arkusz kalkulacyjny może być użyty w celu uproszczenia obliczeń o wysokiej i niskiej wartości.
Metoda najmniejszych kwadratów
Jak ostrzegano, metoda wysoka-niska low może być dość myląca. Powodem jest to, że dane o kosztach rzadko są tak liniowe, jak przedstawiono na poprzedniej ilustracji, a wnioski oparte są tylko na dwóch obserwacjach (z których każda może być anomalią statystyczną lub „wartością odstającą”). W większości przypadków należy zastosować bardziej precyzyjne narzędzie analityczne. Jeśli studiowałeś metody statystyczne, przypomnij sobie „analizę regresji” lub „metodę najmniejszych kwadratów”. To narzędzie idealnie nadaje się do analizy zachowania kosztów. Ta metoda wydaje się narzucająco złożona, ale nie jest tak skomplikowana, jak się wydaje. Zacznijmy od rozważenia celu tego obliczenia. Celem najmniejszych kwadratów jest zdefiniowanie linii tak, aby pasowała przez zestaw punktów na wykresie, gdzie skumulowana suma kwadratowych odległości między punktami a linią jest zminimalizowana (stąd nazwa „najmniejszych kwadratów”). Po prostu, jeśli wytyczasz linię prostego pociągu między wieloma miastami, najmniejsze kwadraty określałyby linię prostą między wszystkimi miastami, tak aby skumulowane odległości (kwadrat) z każdego miasta do toru były zminimalizowane. Przeanalizujmy tę metodę, zaczynając od definicji linii. Linię na wykresie można zdefiniować poprzez jej przecięcie z osią pionową (Y) i nachylenie wzdłuż osi poziomej (X). Na poniższym diagramie obserwuj czerwoną linię rozpoczynającą się na osi Y (o wartości „2”) i podnoszącą się delikatnie w górę, gdy się porusza wzdłuż osi X. Tempo wzrostu nazywa się nachyleniem linii; w tym przypadku nachylenie wynosi 0,8, ponieważ linia „unosi” 8 jednostek na osi Y na każde 10 jednostek „biegu” wzdłuż osi X.
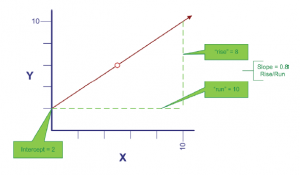
Zasadniczo za pomocą tej formuły można zdefiniować linię prostą:
Y = a + bX
gdzie:
a = punkt przecięcia na osi Y.
b = nachylenie linii
X = pozycja na osi X.
W przypadku linii narysowanej na poprzedniej stronie formuła wyglądałaby następująco:
Y = 2 + 0,8X
A jeśli chcesz poznać wartość Y, gdy X wynosi 5 (patrz czerwone kółko na linii), wykonujesz
następujące obliczenia:
Y = 2 + (0,8 * 5) = 6
Teraz przejdźmy do dopasowania linii przez zestaw punktów. Dalej znajduje się tabela danych pokazująca miesięczną produkcję jednostkową i związany z nią koszt (posortowane od niskiej do wysokiej). Dane te wykreślono na wykresie po prawej stronie. Przez środek punktów danych jest rysowana linia, a linia ma wzór:
Y = 138 533 USD + 10,34 USD
Ta formuła sugeruje, że koszty stałe wynoszą 138 533 USD, a koszty zmienne 10,34 USD za jednostkę. Na przykład, ile kosztowałoby wyprodukowanie około 110 000 sztuk? Odpowiedź to około 1 275 000 $
(138 583 USD + (10,34 * 110 000 USD)).
Jak powstała formuła? Jednym podejściem byłaby „gałka oczna punktów” i narysowanie linii przez nie. Następnie oszacujesz nachylenie linii i przecięcie Y. To podejście jest znane jako metoda wykresu rozrzutu, ale nie byłaby precyzyjna. Dokładniejszym podejściem i tym, które posłużyło do wyprowadzenia powyższej formuły, byłaby technika najmniejszych kwadratów. Przy najmniejszych kwadratach odległość w pionie między każdym punktem a linią wynikową jest kwadratowa, a wszystkie wartości kwadratowe są sumowane. Co ważne, zdefiniowana linia to ta, która minimalizuje zsumowane wartości do kwadratu! Ta linia jest uważana za linię najlepiej dopasowaną, miejmy nadzieję, że daje najbardziej wyraźne wskazanie części stałej (punkt przecięcia) i części zmiennej (nachylenie) obserwowanych danych.
Zawsze można dopasować linię do danych, ale jak wiarygodna lub dokładna jest ta wynikowa linia? Wartość R-Square to obliczenie statystyczne, które charakteryzuje, jak dobrze dana linia pasuje do zestawu danych. Na ilustracji zwróć uwagę (w komórce B21) na R2 wynoszącą 0,798; co oznacza, że prawie 80% zmienności kosztów można wytłumaczyć wahaniami wielkości. Zasadą jest, że im bliżej R2 jest 1,00, tym lepiej; ponieważ byłoby to idealne dopasowanie, w którym każdy punkt przypadałby dokładnie na wynikową linię.
Metoda R-Square jest dobra w teorii. Ale w jaki sposób można znaleźć linię, która powoduje minimalizację skumulowanych kwadratowych odległości od punktów do linii? Jednym ze sposobów jest wykorzystanie wbudowanych narzędzi w programach arkuszy kalkulacyjnych, jak pokazano.
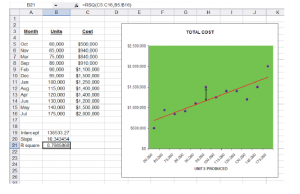
Zauważ, że formuła dla komórki B21 (jak zaznaczono na górze arkusza kalkulacyjnego) zawiera funkcję RSQ (C5: C16, B5: B16). To mówi arkusz kalkulacyjny
obliczyć wartość R2 dla danych we wskazanych zakresach. ikewise, komórka B20 oparta jest na funkcji NACHYLENIE (C5: C16, B5: B16). Komórka B19 to INTERCEPT (C5: C16, B5: B16). Większość arkuszy kalkulacyjnych zapewnia intuicyjność
wyskakujące okna z monitami o skonfigurowanie tych funkcji statystycznych. Arkusze kalkulacyjne nie zawsze były dostępne. Być może ciekawi Cię podstawowa mechanika metody najmniejszych kwadratów. Jeśli tak, możesz sprawdzić link na stronie internetowej.
Podsumowanie
Zanim przejdziemy dalej, przejrzyjmy kilka kluczowych punktów. Dobry menedżer musi zrozumieć strukturę kosztów organizacji. Wymaga to starannego rozważenia składników zmiennych i kosztów stałych. Jednak czasami trudno jest ustalić dokładną strukturę kosztów. W rezultacie można zastosować różne metody analizy zachowania kosztów. Po zrozumieniu struktury kosztów zrganizacji staje się możliwe wykonanie ważnych obliczeń diagnostycznych, które są przedmiotem następnych sekcji.