https://www.remigiuszkurczab.pl/aspergeraut.php
Zauważyłeś, że definicje q1 i q2 zależą od punktu widzenia konkretnej osoby. Załóżmy na przykład, że Janet siedzi tuż za Johnem. John zasłania Janet widok na kinowy ekran i przypadkowo śni na jawie o Janet. Janet jednak nie rozpoznała Johna. Z punktu widzenia Janet relacja z Janem ma wysokie q2 i niskie q1, podczas gdy z punktu widzenia Jana ma wysokie q1 i niskie q2. W rzeczywistości, gdyby normalne użycie języka angielskiego nie uważało, że dwoje ludzi ma ze sobą tylko jeden związek w danym momencie, moglibyśmy powiedzieć, że mieli dwa odrębne związki, po jednym. Na marginesie warto zauważyć, że normalne użycie języka angielskiego na temat relacji międzyludzkich jest w dużej mierze definiowane przez kobiety i to one najczęściej go używają. Tak się składa, że relacje między kobietami są bardziej symetryczne (lub prawie symetryczne) pod względem q1 i q2 niż relacje między mężczyznami. W rezultacie kobiety mogą mówić o związku samym w sobie jako bliskim lub odległym, ciepłym lub zimnym, bez konieczności rozróżniania między dwoma jego końcami. Tak czy inaczej, kiedy rysujemy wykres przestrzeni relacji, zaczynamy od jednego węzła reprezentującego jedną osobę, a następnie dodajemy relacje tej osoby postrzegane przez tę osobę. Wartości q1 i q2 są pokazane obok każdej relacji, której dotyczą. Na przykład, gdybyśmy byli zainteresowani punktem widzenia osoby B, moglibyśmy zacząć jak na rycinie 2.3, gdzie x1 i x2 reprezentują wartości q1 i q2 postrzegane przez B w odniesieniu do A, y1 i y2 reprezentują ich wartości w odniesieniu do C i z1 i z2 reprezentują je w odniesieniu do D. Przekształcając dla arytmofobów, x1 mówi nam, ile A perystatuje B, x2, jak bardzo A epistatyzuje B, y1, jak bardzo C perystatuje B, itd. Jeśli A stoi przed B, próbując coś jej sprzedać, to możemy powiedzieć, że x2 jest większe niż x1. Jeśli B częściej dzwoni do C niż do D, to możemy powiedzieć, że y1 jest większe niż z1. Jeśli w określonym czasie ani C, ani Dis z B, ani rozmowa z nią przez telefon, to możemy powiedzieć, że y2 i z2 są prawdopodobnie równe zeru. Jednakże, jeśli B odczytuje literę z D, to można uznać, że z1 ma wartość większą od zera tak długo, jak uwaga B jest skupiona na tej literze. Jeśli następnie chcemy spojrzeć na związek między, powiedzmy, A i C, mamy dwie możliwości:
- albo możemy zacząć od nowa z nowym wykresem zaczynającym się na literę A lub C
- lub możemy pozwolić B spekulować na temat relacji A/C. (Jeżeli B jest kobietą, to prawdopodobnie zrobiła kiedyś taką spekulację, choćby z tyłu głowy).
Jeśli przyjmiemy drugie podejście, możemy wypełnić nasz wykres jak na rysunku
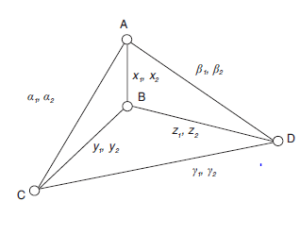
Gdyby jednak A nigdy nie spotkało C i D, wówczas dwie krawędzie łączące A z C i D nie byłyby obecne, α1, α2, β1 i β2 byłyby nieokreślone. Z drugiej strony moglibyśmy dodać jeszcze więcej informacji do wykresu, gdyby B odróżnił pogląd D na C od poglądu C na D i gdyby B spekulował na temat tego, jak A postrzega samą B, w odróżnieniu od tego, jak B widzi A. To dałoby nam co matematycy nazywają grafem „skierowanym”, co oznacza, że krawędzie nie są tylko liniami, ale strzałkami. W naszym przypadku każdą linię można zastąpić parą strzałek, po jednej w każdym kierunku, a każda strzałka miałaby swoje wartości dla q1 i q2. Oprócz pokazania nam, jak bardzo A perystatuje i epistatyzuje B, powiedziałoby nam również, jak bardzo B perystatuje i epistatyzuje A i tak dalej.
Jeśli przyjmiemy drugie podejście, możemy wypełnić nasz wykres jak na rysunku 2.4. Gdyby jednak A nigdy nie spotkało C i D, wówczas dwie krawędzie łączące A z C i D nie byłyby obecne, a 1, 2, 1 i 2 byłyby nieokreślone. Z drugiej strony moglibyśmy dodać jeszcze więcej informacji do wykresu, gdyby B odróżnił pogląd D na C od poglądu C na D i gdyby B spekulował na temat tego, jak A postrzega samą B, w odróżnieniu od tego, jak B widzi A. To dałoby nam co matematycy nazywają grafem „skierowanym”, co oznacza, że krawędzie nie są tylko liniami, ale strzałkami. W naszym przypadku każdą linię można zastąpić parą strzałek, po jednej w każdym kierunku, a każda strzałka miałaby swoje wartości dla q1 i q2. Oprócz pokazania nam, jak bardzo A perystatuje i epistatyzuje B, powiedziałoby nam również, jak bardzo B perystatuje i epistatyzuje A i tak dalej. Wszystko to wyglądałoby bardzo podobnie do wielkiej masy linii z literami i cyframi obok nich. Jeśli naprawdę chcesz to zobaczyć, narysuj to sam.